Искусственные нейронные сети (ИНС) — это упрощенные математические модели организации реальных биологических нейронных сетей (БНС). Пока что ИНС еще очень далеки от возможностей человеческого мозга и мышления, однако уже сейчас нейросети успешно применяются во многих сферах деятельности человека таких как распознавание, а также синтез речи и изображений, роботы-курьеры, беспилотный транспорт, прогнозирование временных рядов и др.

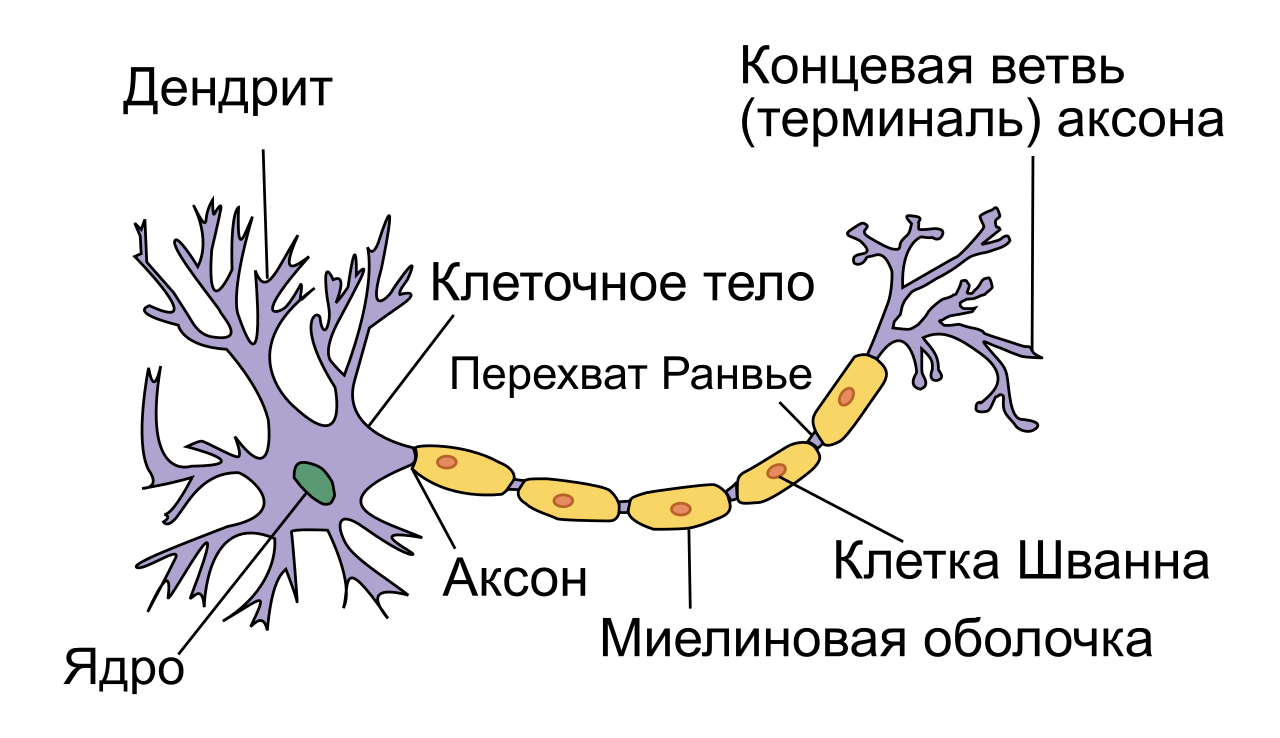
Базовый элемент нейросети — нейрон. Как мы видим на рисунке ниже, структуру биологического нейрона можно упростить до следующей: дендриты, тело нейрона и аксон. Дендриты — ветвящиеся отростки, собирающие информацию со входа в нейрон (это может быть внешняя информация с рецепторов, или внутренняя информация от другого нейрона). В том случае, если входящая информация активировала нейрон (в биологическом случае — потенциал стал выше какого-то порога), рождается волна возбуждения, которая распространяется по мембране тела нейрона, а затем через аксон, посредством выброса нейромедиатора, передает сигнал другим нервным клетками или тканям.

Сначала будет немного математики, потом собственно код.

ТЕОРИЯ

Уоррен Мак-Каллок и Уолтер Питтс в 1943 году предложили модель математического нейрона. А в 1958 году Френк Розенблатт на основе нейрона Мак-Каллока-Питтса создал компьютерную программу, а затем и физическое устройство — перцептрон. С этого и началась история искусственных нейронных сетей. Теперь рассмотрим математическую модель нейрона, с которым мы будем иметь дело дальше. На вход подаются числа (сигналы), после они умножаются на веса (каждый сигнал – на свой вес) и суммируются. К результату суммирования иногда еще добавляют какую-то константу смещения (для упрощения на рисунке смещение отсутствует). Затем функция активации высчитывает выходной сигнал и подает его на выход.

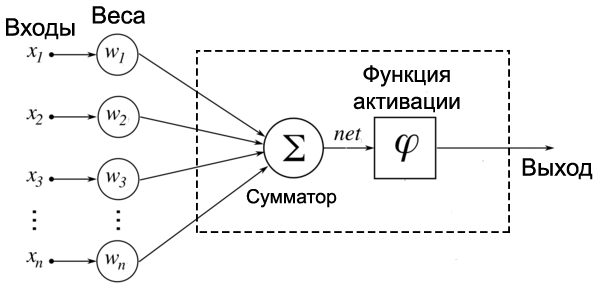
Идея функции активации также взята из биологии. Функция активации позволяет проходить или не проходить сигналам от нейрона к нейронам в зависимости от информации, которую они передают. Т.е. если информация является важной, то функция пропускает ее, а если информации мало или она недостоверна, то функция активации не позволяет ей пройти дальше.

Функции активации бывают очень разные, выбор обуславливается областью применения ИНС и является важной исследовательской задачей для специалиста по машинному обучению. Вот так например выглядят некоторые из них:

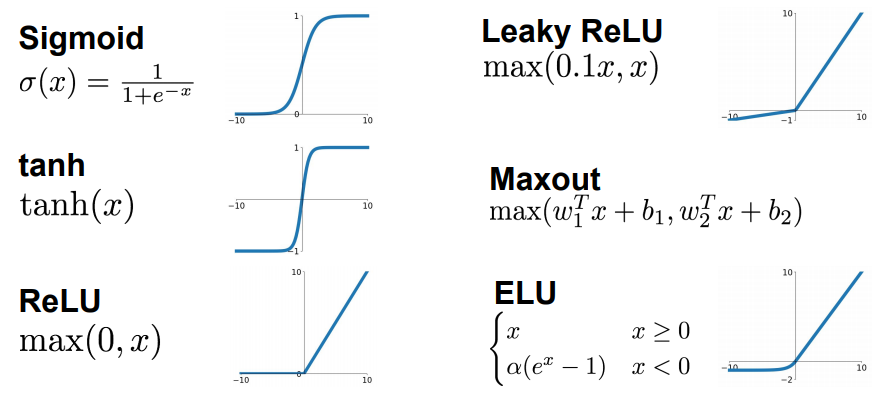
Очевидно, что в самом простом случае вся нейросеть может быть представлена одним единственным нейроном. При этом даже один нейрон хорошо справляется с задачей распознавания класса объекта в пространстве, в котором объекты этих классов являются линейно сепарабельными. Простым примером линейной сепарабельности являются булевы функции OR и AND, для таких функций всегда можно провести прямую (или гиперплоскость в многомерном пространстве), отделяющую 0 значения от 1. А вот с функцией XOR дела обстоят немного сложнее и сеть из одного нейрона с такой задачей увы не справится.

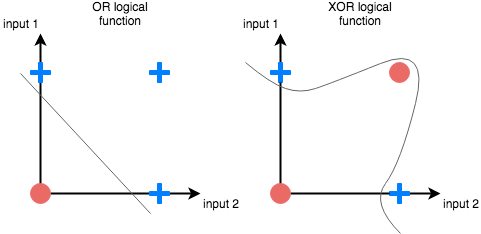
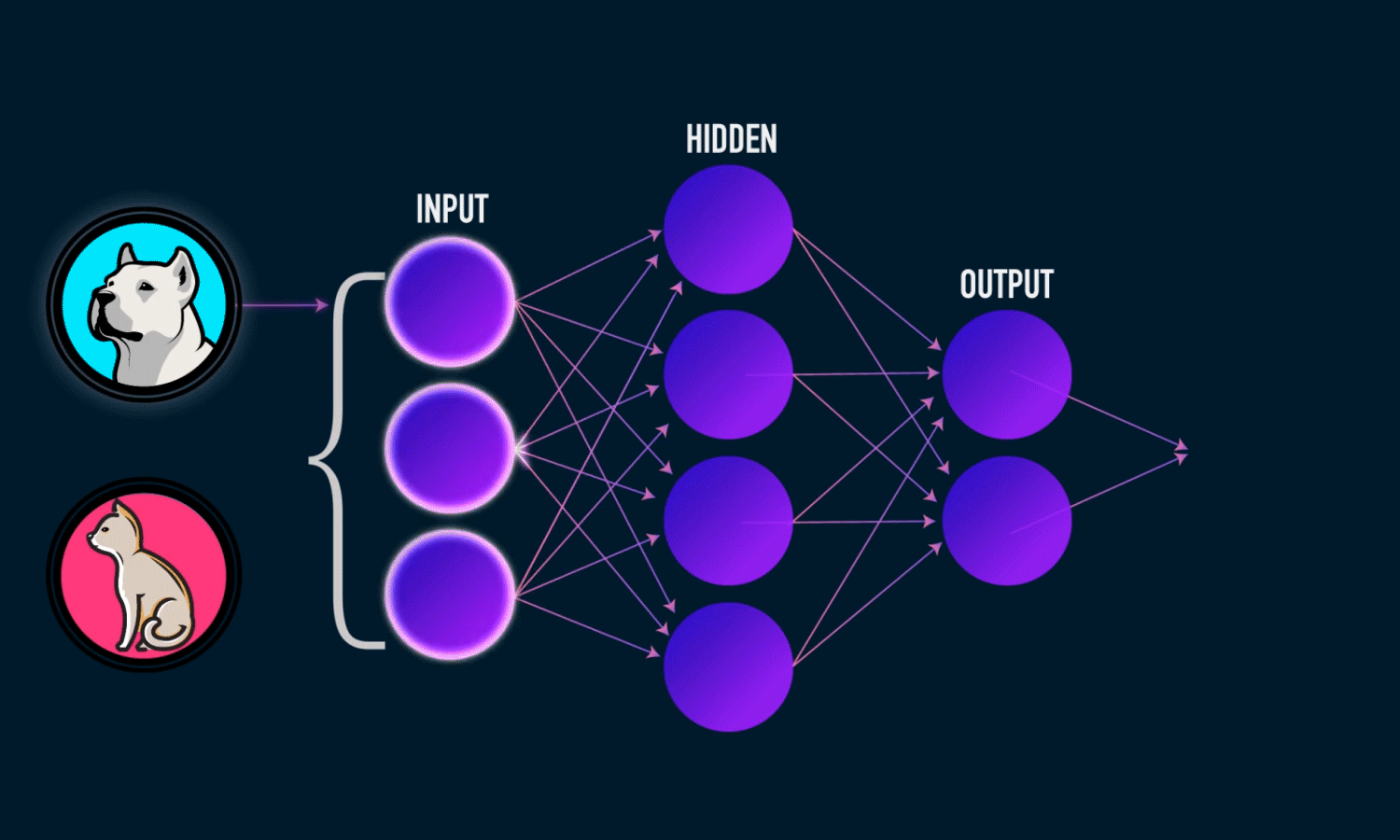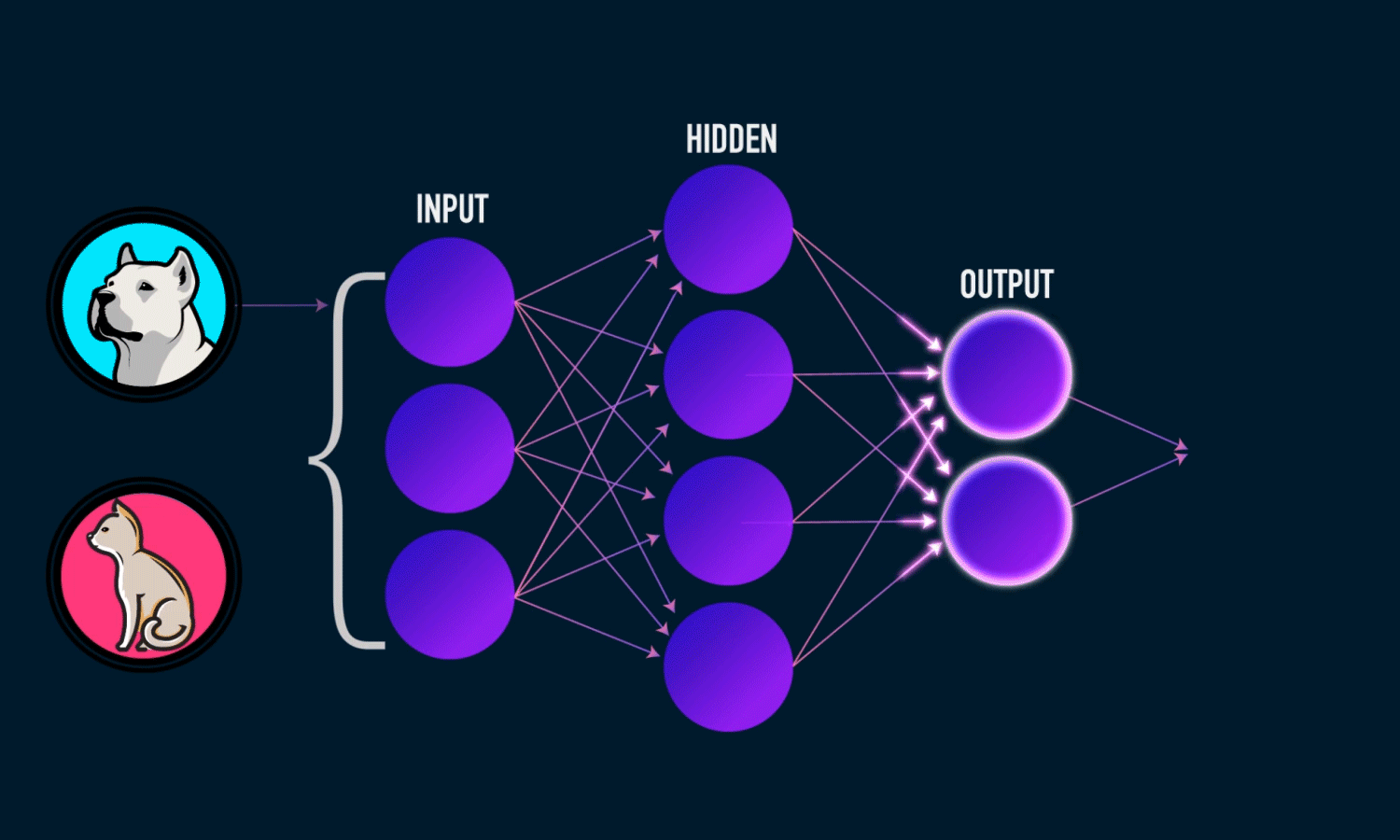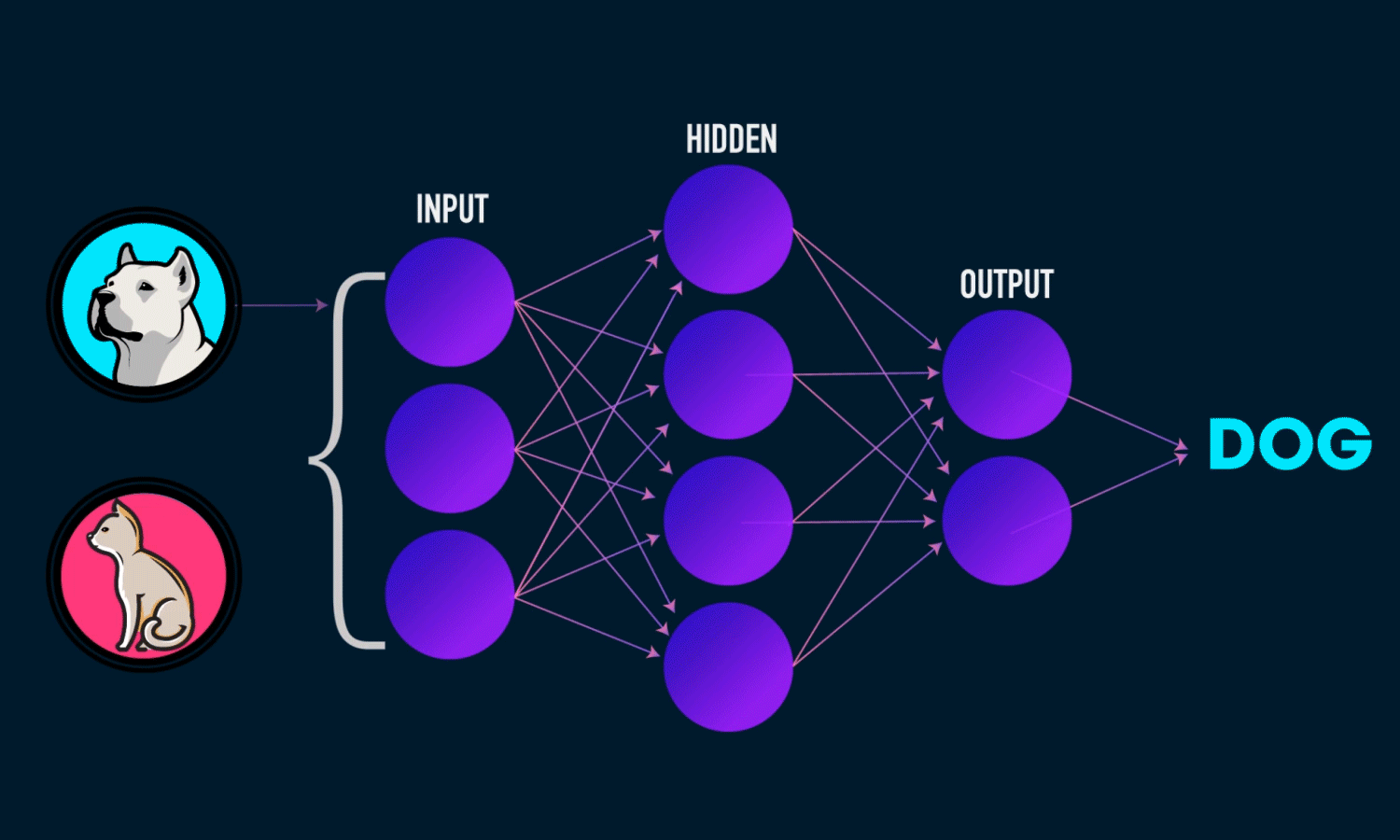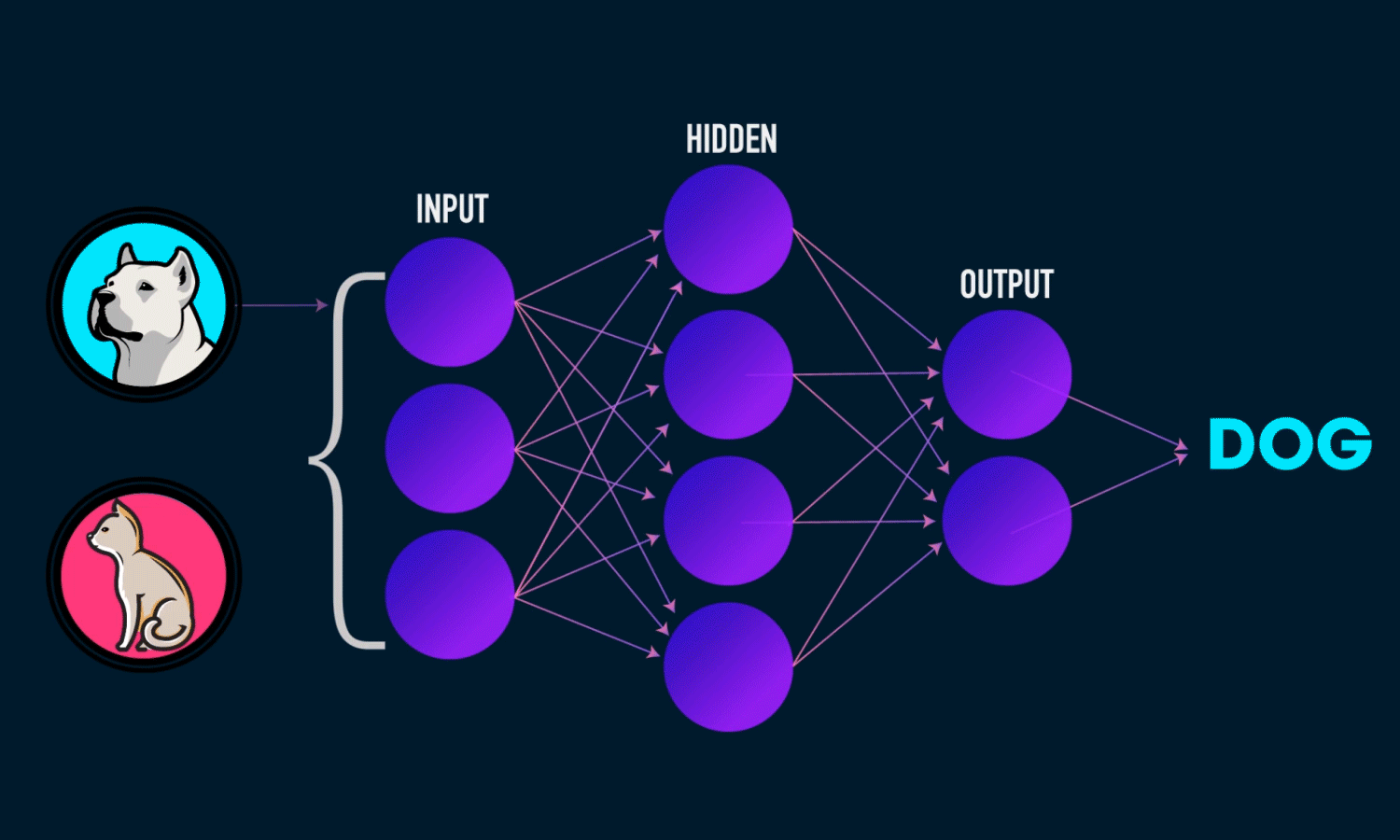
Невозможно провести одну прямую таким образом, чтобы разделить значения исключающего ИЛИ. К счастью, решение достаточно простое. Для этого существуют более сложные архитектуры нейронных сетей, состоящие из множества таких нейронов, объединенных в слои. Такие многослойные сети еще называют глубокими. Им под силу решать сложные задачи, с которыми не может справиться перцептрон. В частности, линейно неразделимые задачи. Графически многослойный перцептрон с одним скрытым слоем выглядит вот так:

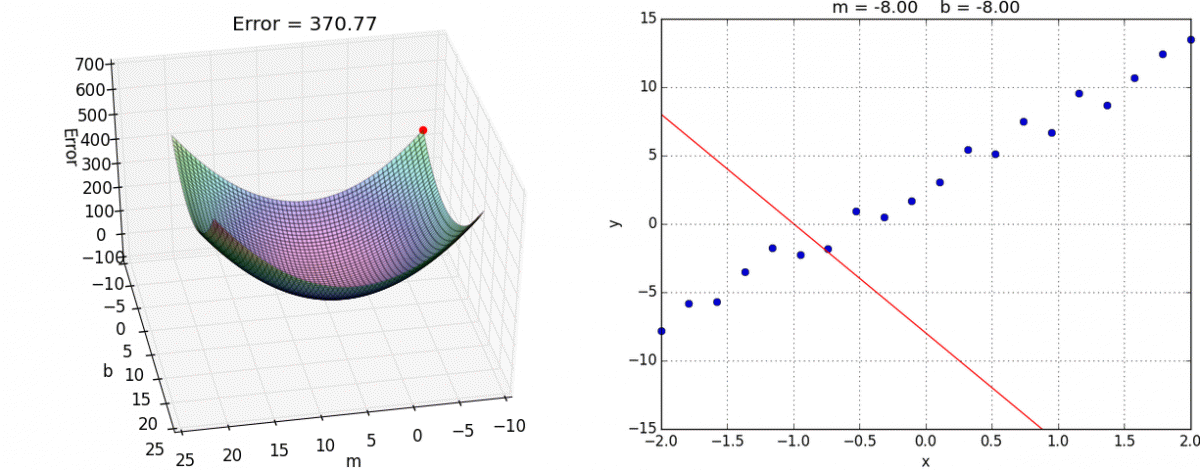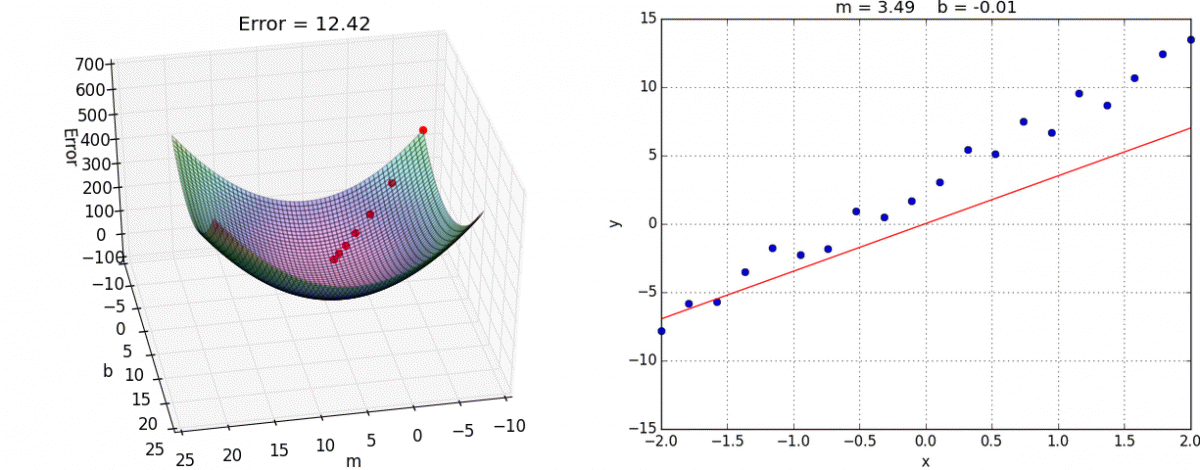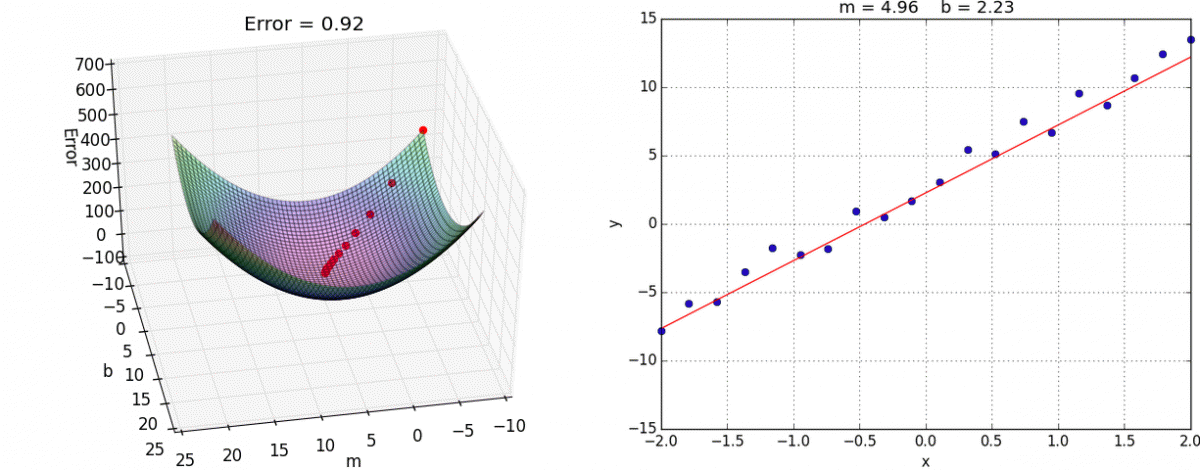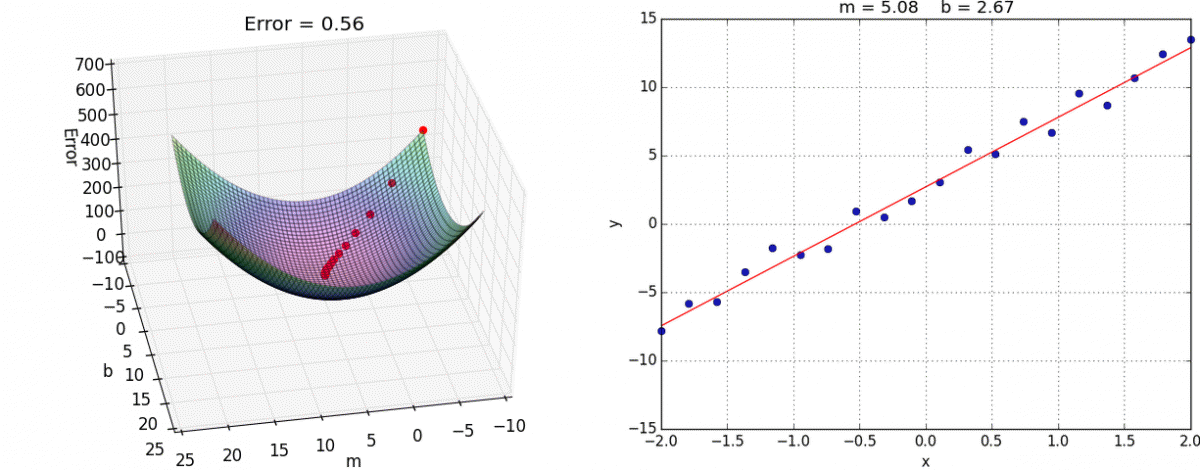
Перед тем как приступить к практике пару слов о том как обучить нейросеть. Как правильно подобрать веса для нейронов так, чтобы ошибка на выходе была минимальной ? Обычно веса инициализируются случайным образом. В процессе обучения значения весов меняются. На практике сейчас наиболее часто применяют метод градиентного спуска и обратного распространения ошибки. Множество библиотек машинного обучения например Tensorflow, Pytorch и др. дают возможность с легкостью реализовать обучение этим методом, не вдаваясь в подробности его реализации. Градиентный спуск — метод нахождения минимального значения функции ошибки (существует множество видов этой функции). Минимизация любой функции означает поиск самой глубокой впадины в этой функции.

Итак у нас есть исходные матрицы весов, мы хотим внести в них изменения, которые делают нашу модель лучше, уменьшают ошибку. Еще у нас есть набор данных для обучения, который состоит из входных данных, и того что мы хотим получать на выходе нейронной сети. Также есть некая фиксированная функция для численной оценки ошибки на выходе. Если будет известно, насколько влияют веса на эту функцию, то будет известно, насколько их нужно изменить. Тут нам поможет частная производная функции ошибки — градиент. Производная позволяет определить крутизну и направление функции при заданном аргументе. Если частная производная известна, можно приступать к обучению сети, которое состоит из двух шагов:

• прямое распространение — обучающие данные подаются на вход сети, проходят через все веса, результаты сравниваются с желаемыми целевыми значеними и таким образом вычисляется текущая ошибка сети

• обратное распространение — зная величину ошибки сети и частную производную, которая вычисляется по каждому весу, веса корректируются с учетом некоего небольшого коэффициента начиная с весов выходных нейронов

Повторять эти шаги нужно итеративно, до тех пор пока ошибка не перестанет уменьшаться. Двигаясь по направлению градиента мы будем плавно скатываться в низину, а динамика обучения нейронной сети напоминает шарик, постепенно скатывающийся в локальный минимум.

ПРАКТИКА

Тут мы обучим многослойный перцептрон выполнять функцию XOR. Обучать будем в Tensorflow (не принципиально, можно использовать любую другую библиотеку машинного обучения). Обученную модель развернем на микроконтроллере с C++ компилятором.

MSP430.js | ноутбук | исходники

Чтобы обучить нейронную сеть, нам понадобится исходный набор данных, в нашем случае это таблица истинности исключающего или:

X = np.array([[0,0], [0,1], [1,0], [1,1]])
Y = np.array([[0], [1], [1], [0]])

Также нужно создать модель нейронной сети. Пусть это будет перцептрон с одним скрытым слоем из трех нейронов. Функция активации скрытого слоя Relu. Выходной слой состоит из одного нейрона с функцией активации Sigmoid. Два входа:

x = x_in = keras.Input(shape=[2])
x = keras.layers.Dense(3, activation='relu',
                       kernel_regularizer='l2',
                       bias_regularizer='l2')(x)
x = keras.layers.Dense(1, activation='sigmoid')(x)
model = keras.Model(inputs=x_in, outputs=x)

Теперь нужно скомпилировать нашу модель, то есть, по существу, настроить ее для обучения. Будем использовать оптимизатор Adam. Оптимизатор — это алгоритм, который изменяет веса и смещения во время обучения. В качестве функции ошибки используем среднеквадратическую ошибку MSE(mean squared error). В нейронный сетях функцию ошибки часто называют функцией потерь:

model.compile(loss='mse', optimizer='adam')

Теперь можно обучить нашу модель. Обучение занимает какое-то время, которое зависит от сложности сети и количестве обучающих данных. В нашем случае сеть крошечная, можно обучать на любом компьютере. Более сложные сети целесообразней обучать на хороших видеокартах. Метод fit в качестве аргумента принимает количество эпох. Эпоха — это один проход всех элементов датасета. С каждой эпохой обучения ошибка должна падать вплоть до какого-то разумного предела.

model.fit(X, Y, epochs=10**5, verbose=0)

После обучения сетью уже можно пользоваться. Так как по-умолчанию в процессе создания нейронной сети её веса инициализируются случайным образом, результаты после каждого нового обучения будут немного отличаться от приведенных ниже:

model.predict(X)

Результат:

array(
  [[0.01152042],
   [0.98572624],
   [0.99311346],
   [0.00970006]], dtype=float32)

Теперь немножко линейной алгебры. В частности неплохо бы вспомнить что там нам в институте рассказывали про матрицы. Для начала выведем все значения найденных весов на экран.

for i, l in enumerate(model.layers):
  if l.get_weights():
    arr2str = lambda y: '[%s]' % ', '.join('%0.9g' % x for x in y)
    w, b = l.get_weights()
    print("W{} = {}".format(i, '[%s]' % ', '.join(arr2str(y) for y in w)))
    print("B{} = {}".format(i, arr2str(b)))

Результат:

W1 = [[-0.100219101, 0.0986418799, 0.0540673025], [-0.101571321, 0.055912815, -0.0540193357]]
B1 = [0.101785883, -0.0555998087, -7.84907461e-05]
W2 = [[-85.8035507], [-90.0149384], [87.0291138]]
B2 = [4.28154087]

У нас два слоя с соответствующими весами для каждого из них плюс смещение. Чтобы лучше понимать математику внутри перцептрона давайте отвяжемся от Tensorflow и вычислим все то же самое исходя из уже имеющихся у нас весов:

for x in X:
  # First layer calculation
  L1 = np.dot(x, W1) + B1
  # Relu activation function
  X2 = np.maximum(L1, 0)
  # Second layer calculation
  L2 = np.dot(X2, W2) + B2
  # Sigmoid
  output = 1/(1+np.exp(-L2))
  print(output)

Результат:

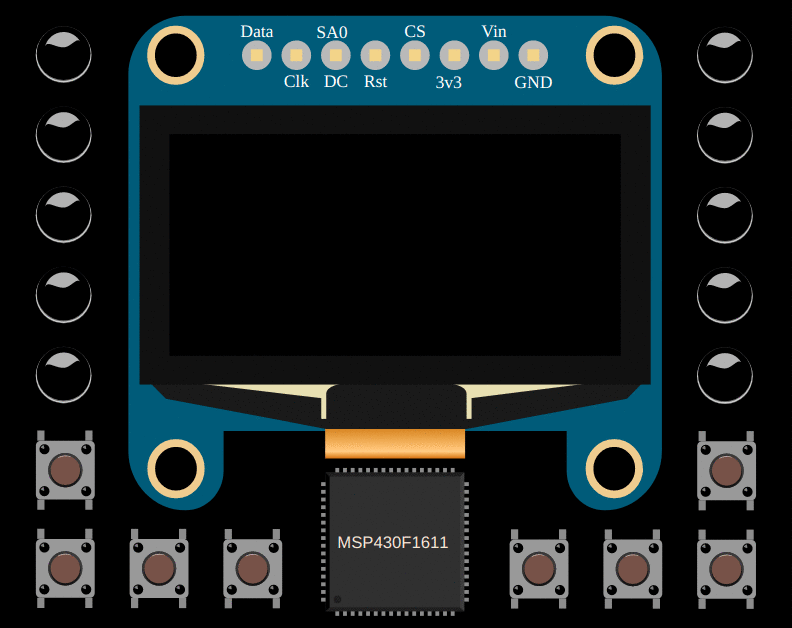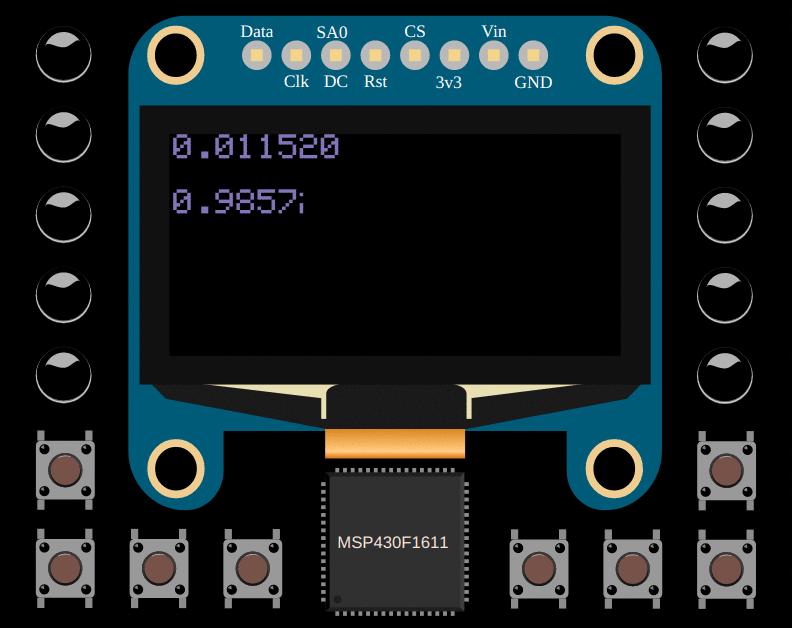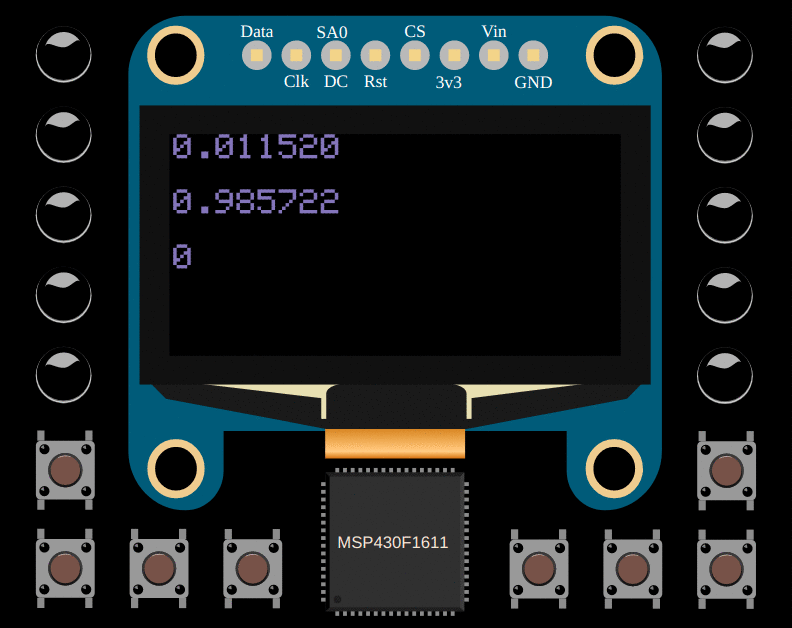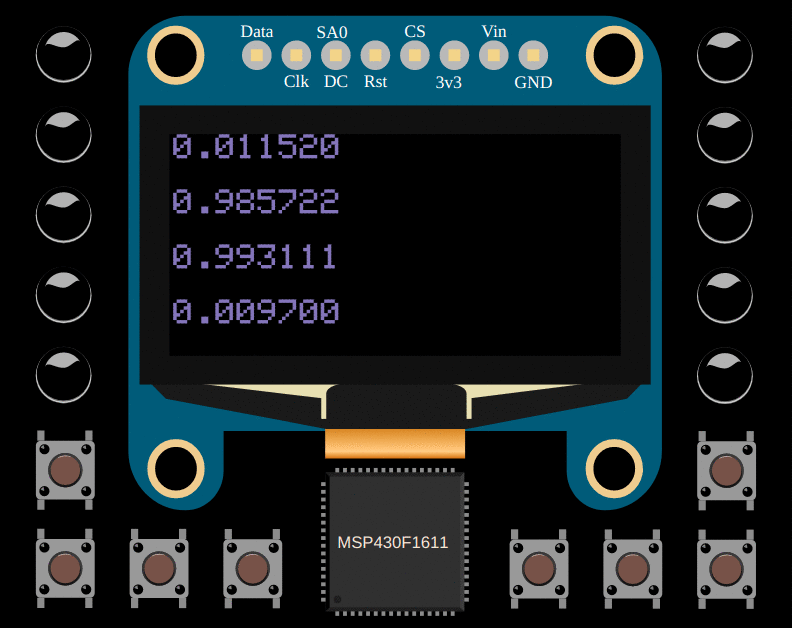
[0.01152039]
[0.98572624]
[0.99311345]
[0.00970005]

Как видим результат полностью совпал с тем, что выдает метод predict в натренированной нами сети. Вычисление выхода слоя заключается в умножении входного вектора на соответствующую весовую матрицу, к результату прибавляется смещение. Затем идет активационная функция. Результирующий вектор умножается на вторую весовую матрицу и т.д.

Думаю математика ясна :) Теперь провернем то же самое, но для микроконтроллера:

nn.h

#include <cmath>
#include <array>

namespace nn {

  template<typename T, size_t N>
  using o = std::array<T, N>;

  template<typename T, size_t N>
  using i = const o<T, N>;

  template<typename T, size_t N, size_t K>
  using m = i<i<T, K>, N>;

  template<typename T, size_t N, size_t K>
  void dot(m<T, N, K> & x, i<T, N> & y, o<T, K> & o)
  {
    for (size_t c = 0, r; c < K; c++)
      for (r = 0, o.at(c) = 0; r < N; r++)
        o.at(c) += x.at(r).at(c) * y.at(r);
  }

  template<typename T, size_t N>
  void relu(o<T, N> & x)
  {
    const T zero = 0;
    for (size_t i = 0; i < N; i++)
      x.at(i) = std::max(x.at(i), zero);
  }

  template<typename T, size_t N>
  void add(i<T, N> & y, o<T, N> & x)
  {
    for (size_t i = 0; i < N; i++)
      x.at(i) = x.at(i) + y.at(i);
  }

  template<typename T, size_t N>
  void sigmoid(o<T, N> & x)
  {
    const T one = 1;
    for (size_t i = 0; i < N; i++)
      x.at(i) = one / (one + std::exp(-x.at(i)));
  }

} // namespace

app.cpp

#include "float32.hpp"
#include "nn.h"
#include "draw.h"

using flt = float32;

static float inference(const flt& x1, const flt& x2)
{
  const nn::m<flt, 2, 3> W1
  {
    -0.100219101, 0.0986418799, 0.0540673025,
    -0.101571321, 0.055912815, -0.0540193357
  };
  const nn::i<flt, 3> B1
  {
    0.101785883, -0.0555998087, -7.84907461e-05
  };
  const nn::m<flt, 3, 1> W2
  {
    -85.8035507, -90.0149384, 87.0291138
  };
  const nn::i<flt, 1> B2
  {
    4.28154087
  };

  // Inputs
  nn::i<flt, 2> x{x1, x2};

  // First layer has 3 units
  nn::o<flt, 3> L1;
  nn::dot(W1, x, L1);
  nn::add(B1, L1);
  nn::relu(L1);

  // Second layer has 1 unit
  nn::o<flt, 1> L2;
  nn::dot(W2, L1, L2);
  nn::add(B2, L2);
  nn::sigmoid(L2);
  return L2.at(0);
}

namespace app {

  int run() {
    draw::flt(draw::PAGE_0, inference(0, 0));
    draw::flt(draw::PAGE_2, inference(0, 1));
    draw::flt(draw::PAGE_4, inference(1, 0));
    draw::flt(draw::PAGE_6, inference(1, 1));
    return 0;
  }
}

Тренировка сложных нейронных сетей может потребовать больших вычислительных мощностей. Здесь на помощь приходят готовые библиотеки для машинного обучения такие как Tensorflow. С их помощью можно обучать нейронные сети на видеокартах, в облаке, и даже в специальных кластерах, состоящих из нескольких вычислительных единиц. Использовать обученную модель можно на где-угодно, даже на очень слабых микроконтроллерах.