Продолжаем осваивать NGSPICE вообще и ОУ в частности.

Интегратор - устройство, уровень выходного сигнала которого пропорционален интегралу (суммы для бесконечного числа бесконечно малых слагаемых), обычно по времени, от входного сигнала. В свою очередь дифференциатор выполняет обратную функцию - уровень выходного сигнала пропорционален скорости изменения сигнала на входе. Аналоговые интегратор и дифференциатор в простейшем случае могут быть реализованы на RC цепочке, т.е. при последовательном включении конденсатора и резистора, но обо всём по порядку. Кстати почему в предыдущем примере RC цепочки фазы входного и выходного сигнала сдвинуты на 90° ? Чему равен интеграл от sin(x) по x ? Чему равна производная от sin(x) ?

~$ echo '
    set term png truecolor size 1280,720
    set xrange [0:2*pi]
    set xtics (0, "π/2" pi/2, "π" pi, "π3/2" 3*pi/2, "2π" 2*pi)
    set grid ytics xtics
    plot sin(x), -cos(x)
    ' | gnuplot > rc.sin.cos.png

Рисовать графики удобно с помощью GnuPlot. Важнейшая особенность синусоидальных сигналов в том, что при дифференцировании/интегрировании форма сигнала не меняется - может измениться только фаза:

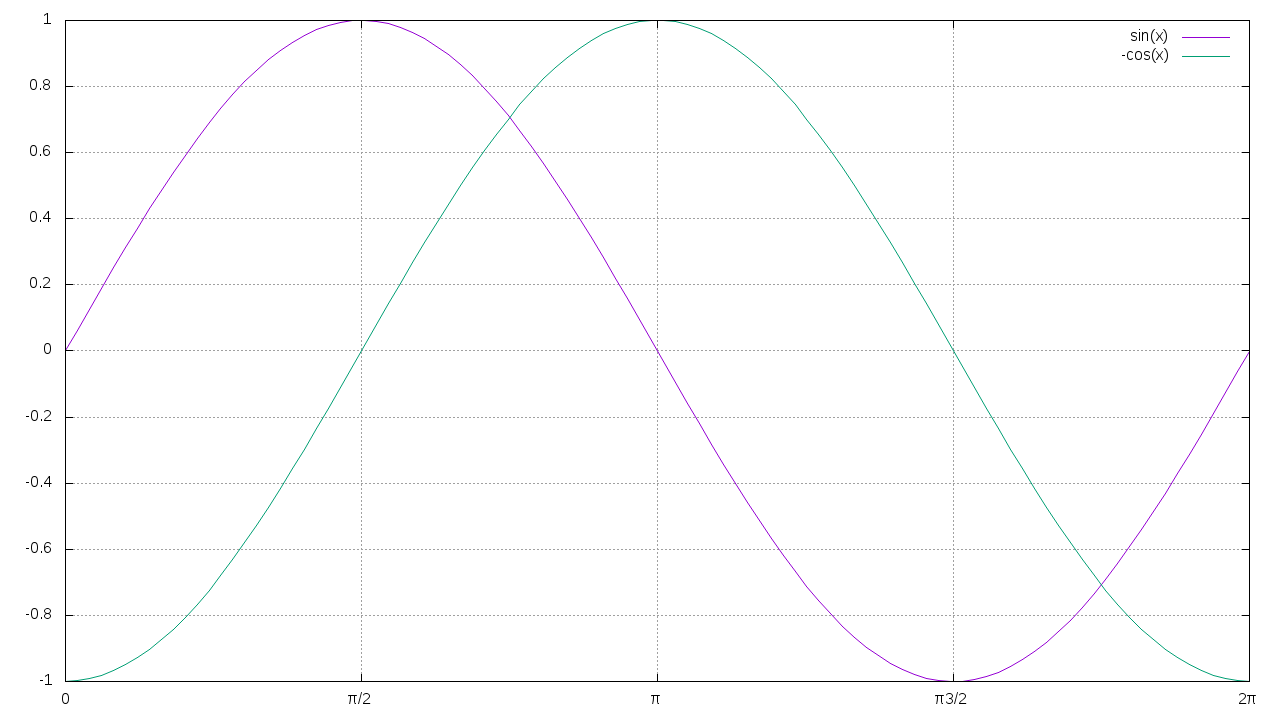
Вспомним немного математики. Как известно из теории электрических цепей в случае последовательного соединения резистора и конденсатора зависимость выходного напряжения от входного описывается дифференциальным уравнением:

Где Uout - напряжение на резисторе в Вольтах, С - ёмкость конденсатора в Фарадах, R - сопротивление резистора в Омах, dUin/dt и dUout/dt - производные входного и выходного напряжений по времени. Какой физический смысл у данного уравнения ?

Самый простой случай - на входе постоянное напряжение, тогда производная dUin/dt равна нулю и формула приводится к виду dUout/Uout = -dt/RC. Проинтегрировав левую и правую часть имеем ∫dUout/Uout = ∫-dt/RC, где ∫dUout/Uout = ln|Uout| + const это табличный интеграл и его умные люди уже давно рассчитали, а ∫-dt/RC = (-t/RC) + const. Окончательно получаем Uout = exp(-t/RC) * const. Порисуем:

~$ echo '
    set term png truecolor size 1280,720
    R=42e3
    C=1e-6
    V=12
    τ=R*C
    set xrange [0:6*τ]
    set xtics ("τ(f)" τ, "2τ" 2*τ, "3τ(%g)" 3*τ, "4τ" 4*τ, "5τ" 5*τ, "6τ" 6*τ)
    set xlabel "Time(second)"
    set ylabel "Voltage(Volt)"
    set grid ytics xtics
    set key center
    plot V*(1-exp(-x/τ)), V*exp(-x/τ)
    ' | gnuplot > rc.tau.png

Если измерять время величинами RC, то график будет всегда одинаков для любой RC цепи. Поэтому величину τ = R*C принято называть постоянной времени. Теоретически напряжение на конденсаторе никогда не достигнет напряжения питания, но на практике считается что времени 5τ и более уже достаточно:

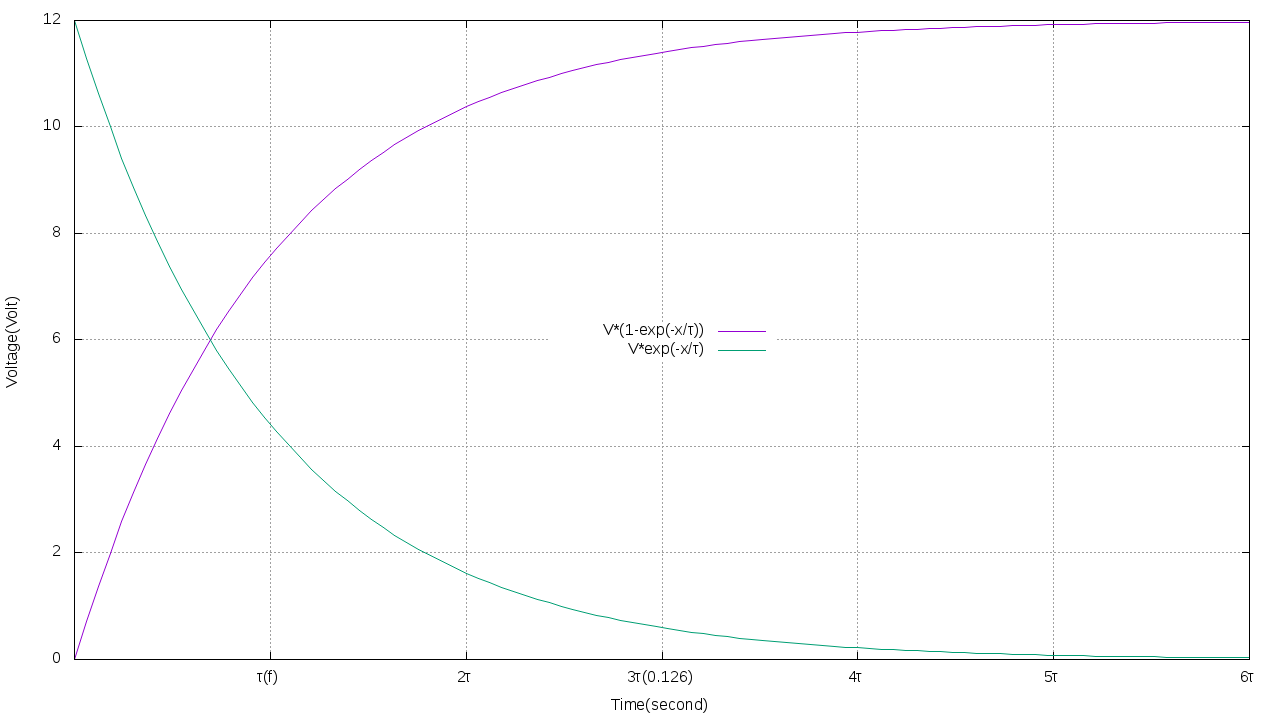
В противоположность к предыдущему случаю предположим, что входное напряжение изменилось с 0 до U за время много меньшее постоянной времени dt << τ. Тогда Uout = τ*dUin/dt - τ*(Uout-0)/dt или Uout = τ*dUin/dt - τ*Uout/dt, а учитывая Uout << τ*Uout/dt можно приблизительно приравнять dUin/dt ≈ dUout/dt, т.е. всё напряжение на входе RC цепочки оседает на резисторе т.к. напряжение на конденсаторе не может измениться мгновенно.

А если входное напряжение изменилось с 0 до U за время много большее постоянной времени dt >> τ ? Тогда Uout >> τ*Uout/dt и можно приблизительно приравнять Uout ≈ τ*dUin/dt, т.е. математически такая RC цепочка выполняет операцию дифференцирования - напряжение на резисторе является производной от функции входного напряжения по времени с коэффициентом τ:

Если теперь выходное напряжение снимать не с резистора, а с емкости, т.е. Uout = Uc, то дифференциальное уравнение примет вид Uout + τ*dUout/dt = Uin. В случае dt >> τ напряжение на конденсаторе повторяет напряжение на входе - по истечении большого промежутка времени Uout ≈ Uin. В случае dt << τ имеем Uin ≈ τ*dUout/dt, такая RC цепочка выполняет операцию интегрирования от функции входного напряжения c коэффициентом 1/τ:

С учётом вышесказанного реальный аналоговый интегратор/дифференциатор должен побороть следующие недостатки простой RC цепочки:

• компенсировать ослабление сигнала, которое происходит при прохождении через RC цепь

• дифференциальные уравнения не учитывают внутреннего сопротивления источника напряжения ровно как и влияния сопротивления нагрузки

С этими обязанностями прекрасно справляется операционный усилитель. В следующих схемах использовалась SPICE модель операционного усилителя LT1007:

~$ wget http://cds.linear.com/docs/en/software-and-simulation/LT1007CS.txt

инвертирующий интегратор на ОУ | netlist | ngspice.js

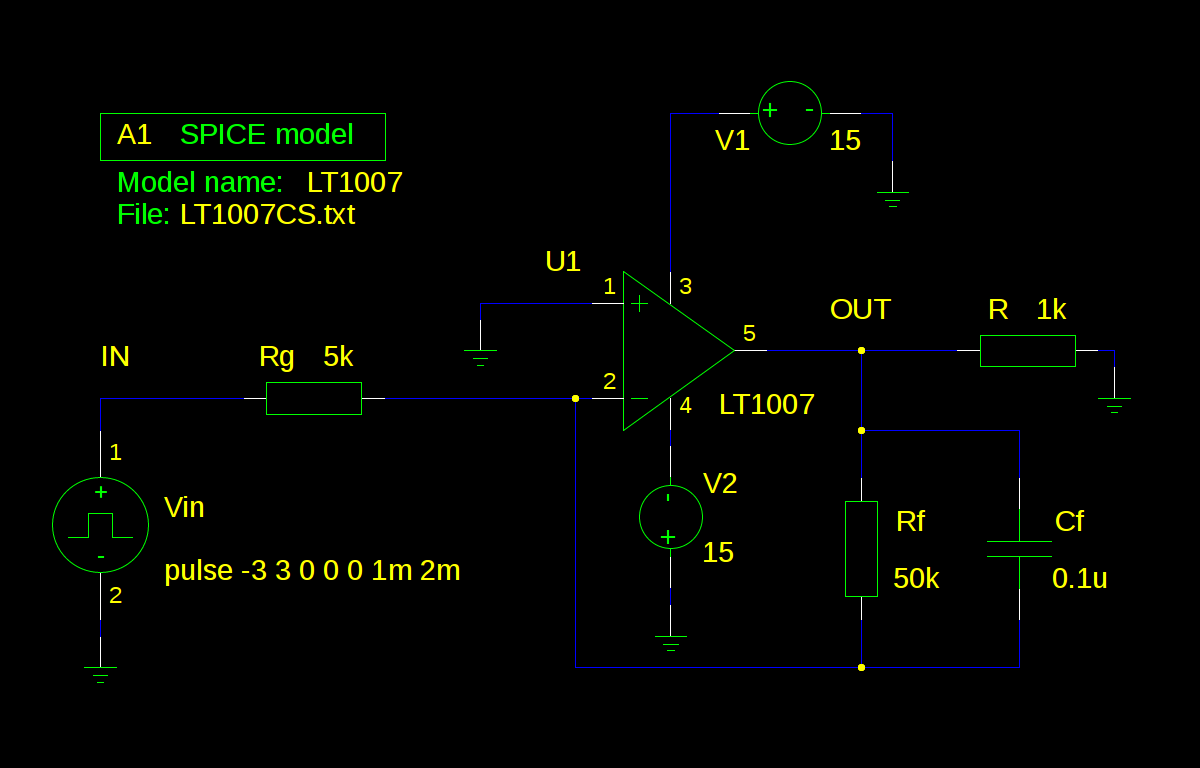
ngspice 1 -> source integrator.net
ngspice 2 -> tran 10u 100m 94m
ngspice 3 -> plot v(out) v(in)

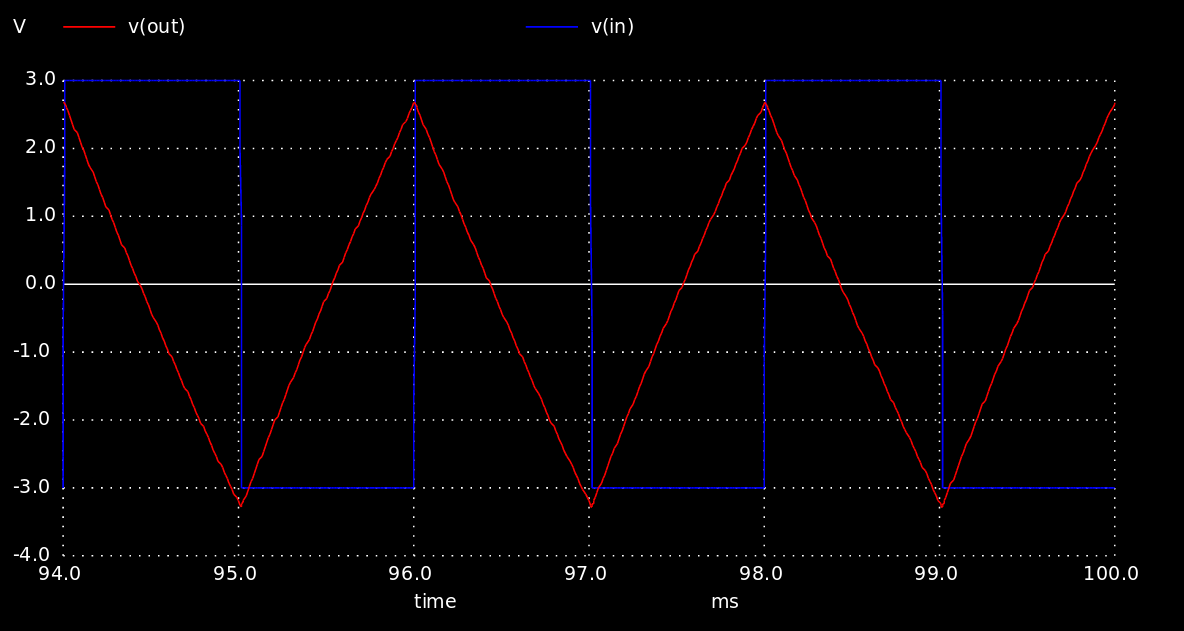
Конденсатор Сf, кроме заряда входным током заряжается различными токами утечки и смещения ОУ и для борьбы с этим явлением ставится шунтирующий резистор Rf, где Rf >> Rg. Рассчитаем поведение интегратора исходя из входного сигнала прямоугольной формы амплитудой 3В и частотой 500Гц при Сf = 0.1мкФ и Rg = 5кОм. Проинтегрировав Uout = -1/RC∫(Uin)dt = -Ut/RC или если человеческим языком, то изменение выходного напряжения во времени представляет собой наклонную прямую с полярностью, противоположной полярности входного сигнала. Интегрированием в пределах от 0 до 1/(2*500Гц)=1мс получим значение Uout = -3*10^-3/(10^-7*5*10^3) = -6 Вольт.

Если на предыдущей схеме всего-навсего поменять резистор и конденсатор местами получим дифференциатор. Для предотвращения самовозбуждения дифференциатора на высоких частотах дополнительно вводятся резистор Rg и конденсатор Cf обычно при соотношении Rg*Cg = Rf*Cf:

инвертирующий дифференциатор на ОУ | netlist | ngspice.js

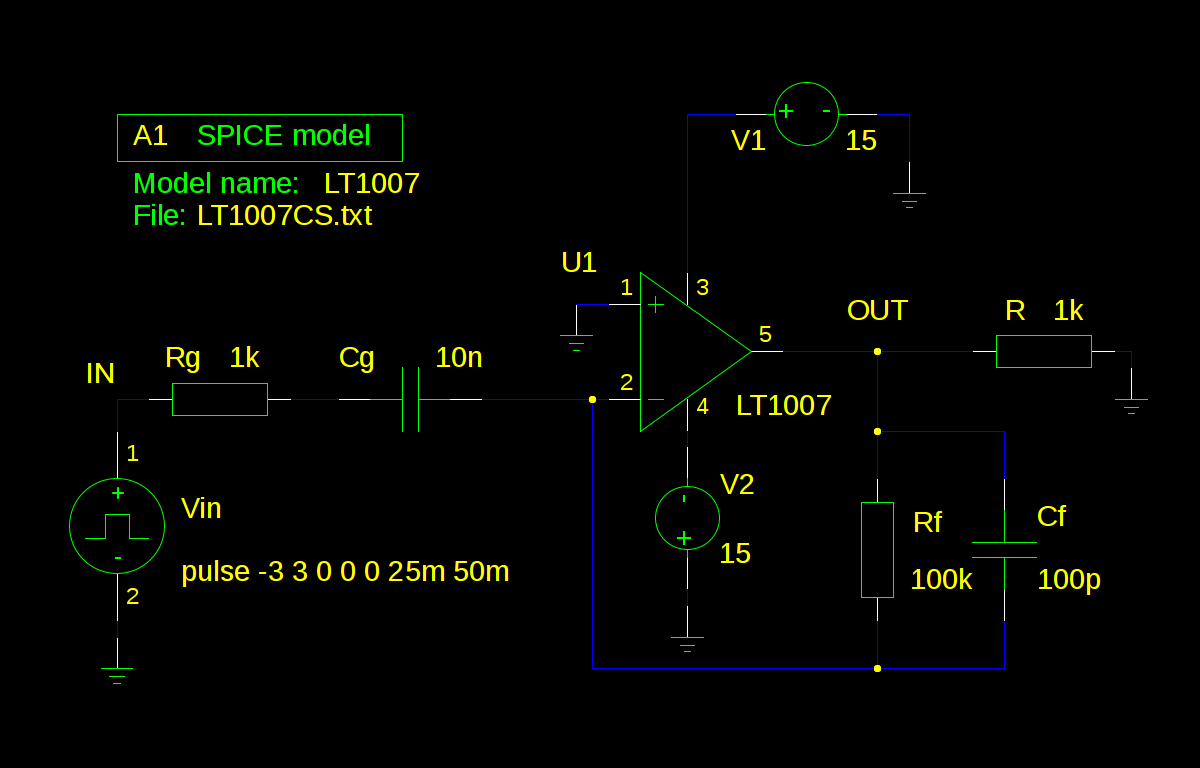
ngspice 1 -> source differentiator.net
ngspice 2 -> tran 0.25m 0.25
ngspice 3 -> plot v(out) v(in)

К недостаткам дифференциаторов прежде всего относится очень большая чувствительность к шумам и помехам у входного сигнала. При резком изменении входного сигнала производная очень большая и ОУ входит в режим насыщения. Получаем такой вот кактус (шутка):

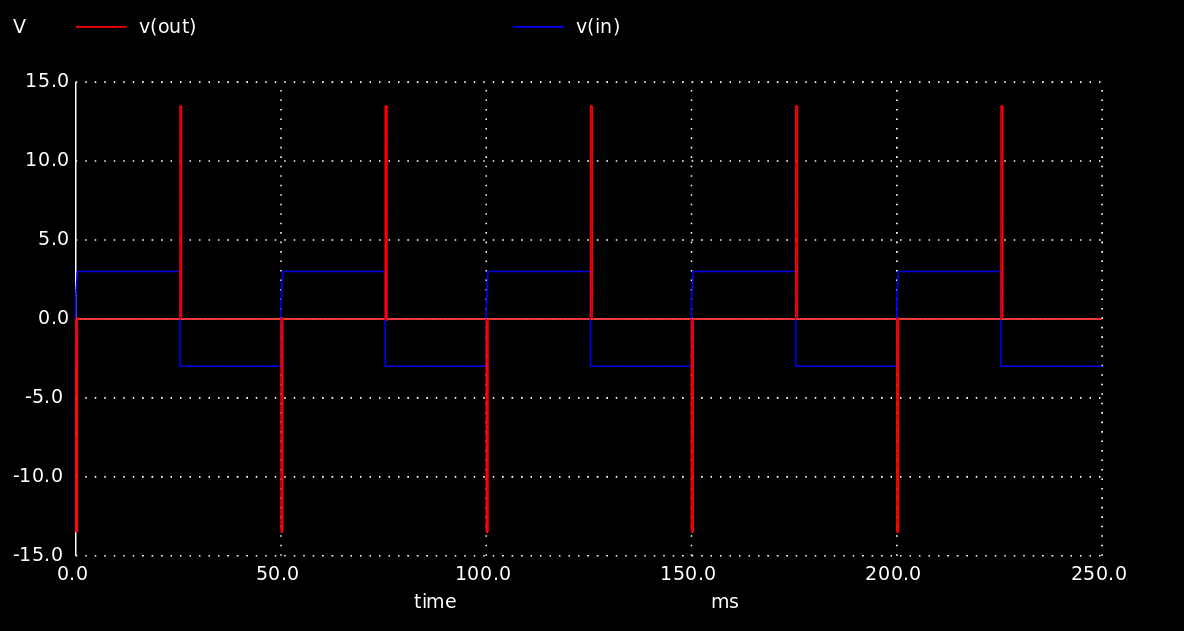
Классическим примером практического применения интегратора и дифференциатора является пропорционально-интегрально-дифференцирующий (ПИД) регулятор.

Далее широтно-импульсная модуляция (ШИМ) и управление коэффициентом заполнения.